干货 | 为以太坊引入 KZG 承诺：工程师视角（下）

干货 | 为以太坊引入 KZG 承诺：工程师视角（上）

（续前）什么是 KZG10 承诺？

注 3.6：如果启动设置所计算的 [s],[s^2]…[s^d] 只计算到了指数 d，这一组值是不能用来生成任何阶数大于 d 的多项式的承诺的。反之亦然。

因为在安全的曲线上，没有办法用两个点相乘来得出第三个点，所以 [s^(d+k)] 是一个（永远！）无法求出的值，因此可以说，任意的承诺 c(f) 都只能表示一个阶数小于等于 d 的多项式。

注 3.7：使用 KZG10 承诺的证据基本上就是在证明 f(x) - 某些余数 的结果可以按特定的办法来分解，但这就要有一种办法可以 相乘 这些因数，并与原始的承诺相比较 C(f)=f([s])。

为此，我们需要 “配对方程”，就是一种能把曲线上的两个点相乘并与另一个曲线点比较的乘法，因为我们无法直接让这两个曲线点直接相乘来得到合成的曲线点。

注 3.8：上述两个属性，可以进一步用来证明某个承诺 c(f) 所代表的多项式 f(x) 的阶数 k 小于 d。

综上，KZG10 承诺可以有很好的属性：

• 验证承诺的过程是：（由区块生成者）提供底层多项式在任意点 r 上的值 y=f(r) ，以及除法多项式 q(x)=(f(x)-y)/(x-r) 在 [s] 点的值（即 q([s])），并用 配对方程 来对比之前所提供的承诺 f[s]。这就叫 开启 在 r 点的承诺，而 q([s]) 就是证据。容易看出，q(s) 就是 p(s)-r 除以 s-r ，恰好就是我们用配对方程来检查的东西，即检查 (f([s])-[y]) * [1]'= q([s]) * [s-r]' （译者注：此处疑为 f(s)-r ，但原文就是 p(s)-r）。
• 在非交互且确定性的版本中， Fiat Shamir Heuristic 提供了一种办法来获得相对随机的点 r：因为随机性只跟我们尝试证明的输入有关，即，只要已经有了承诺 c=f([s]) ，r 就可以用哈希所有输入（r=Hash(C,..)）来获得，而 承诺的提出者 要负责提供 开启点 和 证据。
• 使用预先计算好的拉格朗日多项式，f([s]) 和 q([s]) 都可以在 求值形式 下直接计算。要计算 r 处的开启值，就需要把 f(x) 转为 f(x)=a0+ a1*x^1.... 的系数形式（也即抽取出 a0、a1、…）。可以通过 反向快速傅立叶变换 来实现，复杂度为 O(d log d)，但甚至这里也有一种可用的替代算法，在 O(d) 的复杂度内完成计算，而无需使用反向快速傅立叶变换。
• 你可以使用单个开启点和证据来证明 f(x) 的多个值，也就是多个索引值对应的数值， index1=>value1、index2=>value2 …
• （用于计算证据的）除法多项式 q(x) 现在变成了 f(x) 除以零多项式 z(x) =(x-w^index1)*(x-w^index2)...(x-w^indexk) 的商
• 余数为 r(x) （ r(x) 是一个最大阶数为 k 的多项式，由 index1=>value1, index2=>value2 … indexk=valuek 插值而成）
• 检查 ( f([s])-r([s]) )* [1] ' = q([s]) * z([s]')

• 对任一 索引值 => 数值 点的任何更改，比如更改了 indexk，都需要使用相应的拉格朗日多项式来更新承诺。复杂度约为每次更新 O(1)。
• 但是，因为 f(x) 本身也改变了，所以所有的见证 q_i([s]) ，也即所有对第 i 个键值对的见证，也需要更新。总复杂度约为 O(N)
• 如果我们没有维护预先计算好的 q_i([s]) 见证，任何一条见证数据都要从头开始计算，都需要 O(N)
• 一种复杂度为 sqrt(N) 的更新 KZG10 承诺的构造

Verkle 树

• 每个父节点都编码对其子节点的承诺，子节点就是一个映射，其索引值都存在其父节点内
• 实际上，父节点的承诺编码了哈希后的子节点，因为承诺的输入是标准化的、32 字节的值（见上文的 注3.0）。
• 叶子节点编码了对其所存储的数据的 32 字节哈希值的承诺；或者直接跳转到数据，假如其 32 字节的数据的用法与下一章提到的 状态树 提议用法一样的话。
• 要提供对一个分支的证据（类似于默克尔分支证据）时，一个多值证明的承诺 D、E 可以围绕使用 fiat shamir heruristic 产生一个相对随机的点 t 来生成。

• 更新/插入 叶子节点 index=>value 需要更新 log_d(N) 个承诺 ~ log_d(N)
• 为生成证据，证明者需要
• 计算 f_i(X)/(X-z_i) 在 [s] 处的值，用于生成 D ，复杂度总计 O(d log_d N)，但可以在 更新/插入 时调整以节约预计算，复杂度会变成O d log_d(N)
• 计算 m 个 ～ O( log_d(N) ) 个 f_i(t) 来计算 h(t)，总计为 O (d log_d N)
• 计算 π, ρ ，需要对 m~ log_d N 个指数多项式的和做除法。需要约 O(d log_d N) 来获得分子的求值形式，以计算除法
• 证明的规模（包括用于计算 E 的分支承诺）加上验证的复杂度 ~ O( log_d(N) )

Verkle 树构建

• 把地址和 头/存储空档 结合起来推导出一个 32 字节的 storageKey，本质上就是元组 (address,sub_key,leaf_key) 的一种表示
• 所推导的键的前 30 个字节用于构建普通的 verkle 树节点 pivots
• 后 2 个字节是一个树高为 2 的子树，表示最多 65536 个 32 字节的分块
• 对于基本的数据，这个树高为 2 的子树最多有 4 个叶子承诺，来覆盖 haeader 和 code
• 因为一个分块为 65536*32 字节的分块表示为单个的字数，所以主树上可能有许多子树来存储一个账户
• Gas 定价方案
• 访问类型 (address, sub_key, leaf_key) 的事件
• 每一个专门的访问事件都收取 WITNESS_CHUNK_COST
• 每个专门的 address,sub_key 组合都收取额外的 WITNESS_BRANCH_COST

• 一个区块的 header 和 code 都作为一个树高为 2 的承诺树的一部分
• 单个分块最多有 4 条见证数据，分别收取 WITNESS_CHUNK_COST，访问账户需要收取一次 WITNESS_BRANCH_COST

数据采样和 PoS 协议中的分片

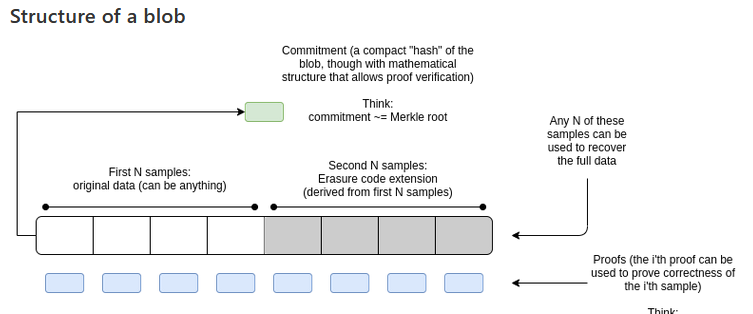
• 分片数据块（不带纠删码）是 16384 个样本（每个 32 字节），约为 512 kb；还有数据头，主要由这些样本相应的最大 16384 阶的多项式承诺组成
• 但多项式求值形式 D 却有 2^16384 的规模，即，1,w^1,…w^,… w^32767，而 W 是 32768 的单元根（不是 16384 的）
• 我们可以为数据（f(w^i)=sample-i for i<16384）拟合出最大 16384 阶的多项式，并扩展到 32768 作为纠删码样本，即计算 f(w^16384) … f(w^32767)
• 对每个点的值的证明也同时计算并与样本一起发布
• 32768 个样本中获得任意 16384 个都可以完全恢复出 f(x) 以及原始的样本，即 f(1),f(w^1),f(w^2)… f(w^16383)
• 这纠删编码的 32768 个样本分为 2048 个分块，每个分块包含 16 个样本，即 512 字节的数据；由分片提议者水平地发布，即将第 i 个分块以及相应地证据发给第 i 个垂直子网络，外加全局公开完整数据的承诺
• 在被指定的 (shard, slot)，每个验证者都在 k~20 个垂直子网中下载和检查这些分块，并使用对应数据块的承诺来验证它们，以建立数据可得性保证
   
• 我们需要为每个 (shard, slot) 安排足够多的验证者，使得总体上一般（乃至更多的数据）都被获取了；另外，还要满足一些统计学上的要求，每个 (shard, slot) 约 128 个委员，需要有至少 70 个（也即 2/3 ）委员的见证，使得该分片数据块能成功打包到信标链上，
• 至少需要约 262144 个验证者（32 个 slot，乘以 64 个分片，再乘上至少 128 个委员）

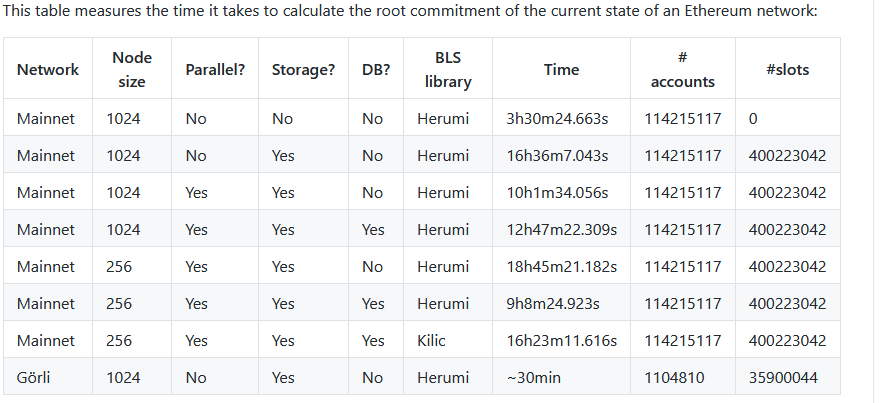
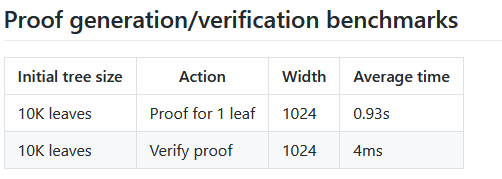
基准测试

原文链接:

https://hackmd.io/yqfI6OPlRZizv9yPaD-8IQ

作者: g11tech

作者：以太坊爱好者；来自链得得内容开放平台“得得号”，本文仅代表作者观点，不代表链得得官方立场凡“得得号”文章，原创性和内容的真实性由投稿人保证，如果稿件因抄袭、作假等行为导致的法律后果，由投稿人本人负责得得号平台发布文章，如有侵权、违规及其他不当言论内容，请广大读者监督，一经证实，平台会立即下线。如遇文章内容问题，请发送至邮箱：linggeqi@chaindd.com